H20NatureOfLight.htm

A ray of light is a flow of energy in the form of an electromagnetic wave. Electromagnetic waves are a special type of oscillation in the magnetic field and the electric field. The oscillations travel through a vacuum at 299,800,000 metres per second, known as the speed of light. The magnetic field and the electric field vectors are at right angles to each other as shown in Figure 1.

Figure 1: The electric and magnetic field variation of an electromagnetic wave travelling through space

The speed of the light is highest when it is in a vacuum and is slower when it is travelling through a material. The ratio of the speed of light in vacuum to that in a material is known as the refractive index (n).

The refractive index of air is 1.00 and of water is 1.33. The refractive index of glass and of most types of polymeric materials, such as plastics and the resins and binders used in paints and inks, is of order 1.50.

The frequency of oscillation of the electric and magnetic fields has the symbol ν. The frequency of a wave is determined when it is emitted and the frequency does not change as the wave passes from one material to another.

The distance between the peaks in the oscillation is the wavelength of the radiation. Electromagnetic radiation with wavelengths in the range from 380 nm to 730 nm can be seen by the human eye and is known as light. A nanometre is a thousand millionth of a metre (10-9 m). Light forms a very narrow range of wavelengths in the spectrum. The full range is from high-energy gamma radiation (very short wavelengths) to low-energy radio waves (very long wavelengths), as illustrated in Figure 2.

The foundations of the understanding of colour are the experiments of Isaac Newton in Cambridge in 1666. Newton used a prism to split sunlight up into a spectrum to show that white sunlight contained all the basic colours. The main bands of colour are shown against wavelength in Figure 2. The wavelength bands associated with the colour names are only approximate since the colours merge smoothly from one to another.

The wavelength of the radiation within a material is determined by the frequency of the radiation and the speed of the light in the material.

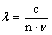
The energy in the wave can be exchanged with materials by inducing movement in the charges in the atoms and molecules within the material. The energy within the light beam behaves as if it contained in small packets. For a given frequency of the light, each packet contains exactly the same amount of energy, known as the quantum of energy. The frequency of the light is related to its energy (E) by the equation

Where h is Planck’s constant (h = 6.626 x 10-34 Js). Thus red light, which has a relatively low frequency (long wavelength), is of a lower energy than blue light, which has a higher frequency (shorter wavelength).

Radiometric terms provide a physical description of the nature of the radiation. The intensity of the light beam is expressed in terms of the energy per unit time crossing a unit area oriented normal to the beam direction, the units are Watts / m2. In the wave model of light, the intensity is proportional to the square of the magnitude of the oscillating electric field. In the particle model of light, the intensity is proportional to the number of particles per second crossing the unit area.

Photometric terms are used to describe the visual brightness (luminance) of a beam or source of light. The luminance is the visual energy per unit time crossing a unit area oriented normal to the beam direction.

How bright a light of a single wavelength appears to the eye depends on both the intensity of the beam and the sensitivity of the eye at that wavelength. Two beams of the same intensity but different wavelengths will appear to the eye to have different brightness. The relative luminosity of the various wavelengths of light with the same radiometric intensity (Watts) is shown in Figure 3.

As can be seen in Figure 3, under normal levels of illumination the eye is most sensitive to green light of wavelength 555 nm. At this wavelength, an intensity of 1 Watt/m2 has a luminance of 683 lumens/m2. If the light were emitted uniformly over the visible spectrum then it would have a luminance of about 200 lumens/m2. Typical illumination levels at the earth's surface are shown in Table 1.

Figure 3: Sensitivity of the eye to different wavelengths of light

The luminous efficiency of a lamp describes the fraction of the electrical energy that is converted to useful visual energy and has the unit of lumens/Watt. The luminous efficiency value depends on the spectral power distribution, the relative energy emitted by the lamp at each wavelength in the visible spectrum. The most efficient of the commonly available types of lamps are fluorescent lamps; the least efficient are tungsten filament lamps (Table 2).

Table 1: Illumination levels at the earth’s surface		Table 2: Efficiency of two of the commonly available types of lamp.
Environment (UK)	lumens/m2		Lamp type and electrical power	lumens	lumens /Watt
Bright summer sunlight	44,000		40 Watt Tungsten filament, gas filled	450	12.25
Overcast daylight	5,000		40 Watt Cool white fluorescent lamp	3150	78.75
North skylight, open shade	4,400

The oscillations in the electric field part of electromagnetic radiation interact strongly with the charges present in atoms and molecules.

When the radiation is polarised, the electric field oscillations are along a particular direction in space, at right angles to the direction of motion. The direction of oscillation is known as the polarisation direction, as illustrated in Figure 4.

Figure 4: Electric field oscillation for horizontally polarised light (left) and vertically polarised light (right)

The "white" light emitted by most types of lamps is un-polarised. Light can be made polarised by passing it through a polarising optical filter. Such a filter transmits all the light that is polarised parallel to a particular direction and absorbs all the light that is polarised at right angles to this direction. The well-known "Polaroid" type of sunglasses has this type of filter for the lens.

Un-polarised light may become partially polarised by scattering from small particles and by reflection at a boundary between two regions of different refractive index. For example, the "glossy" light reflected from the top surface of a high-gloss paint, from a printed material or from the wet surface of a road. One of the advantages of Polaroid sunglasses is that the “glossy” light being absorbed by the lens reduces the “glare” from the shiny surface.

The polarisation properties of light are used in liquid crystal displays. Between the light source and the screen are placed two polarised filters, with polarisation directions perpendicular to each other. Between the two filters is a layer of a nematic liquid crystal sandwiched by two electrodes, one either side. The liquid crystal is able to rotate the direction of polarisation of the light by 90°, as shown in Figure 5.

Figure 5: Polarisation of light in a conventional LCD display screen

In a normal state, light polarised by the first filter passes through the liquid crystal, through the second filter and out of the cell. When a voltage is applied across the electrodes, the orientation of the liquid crystal molecules is altered and the rotation of light polarisation does not occur. The polarised light is now unable to pass through the cell as the second filter absorbs it. This part of the display now looks black.